The Devil's Staircase

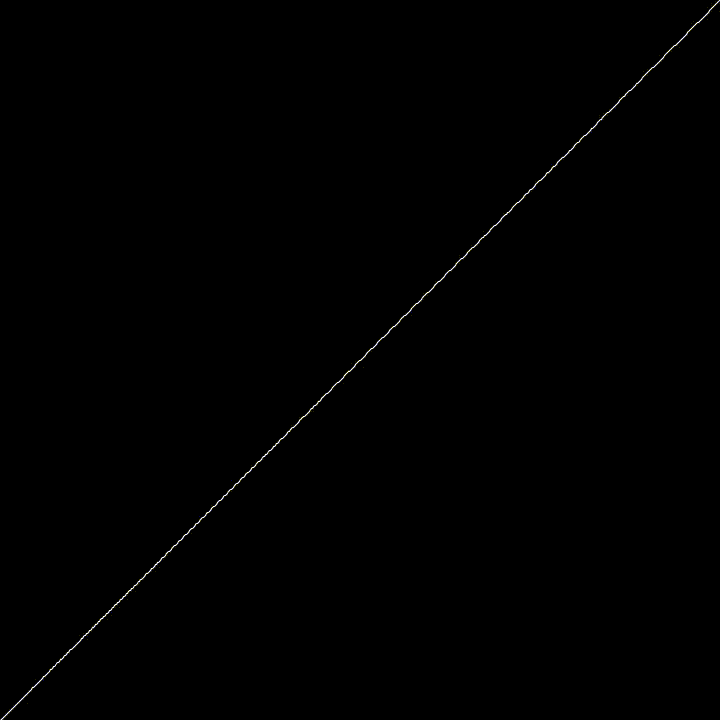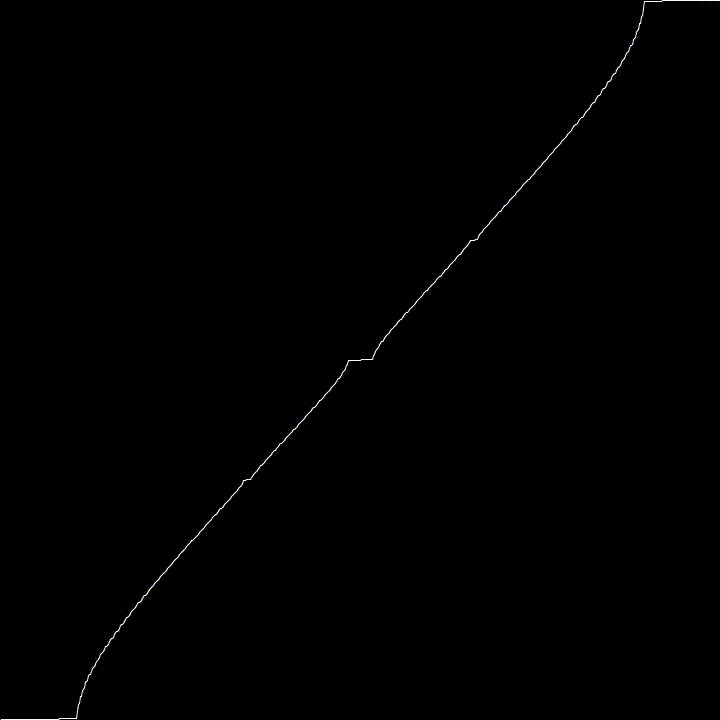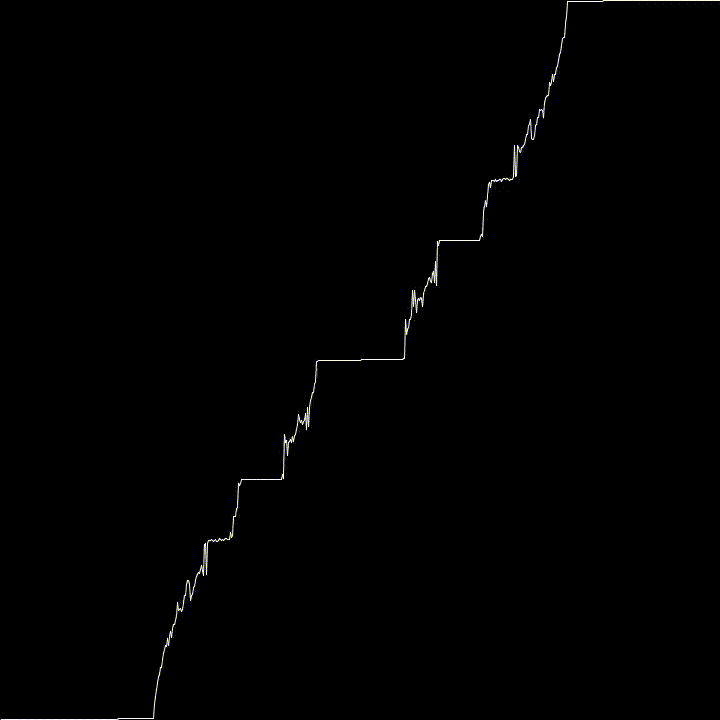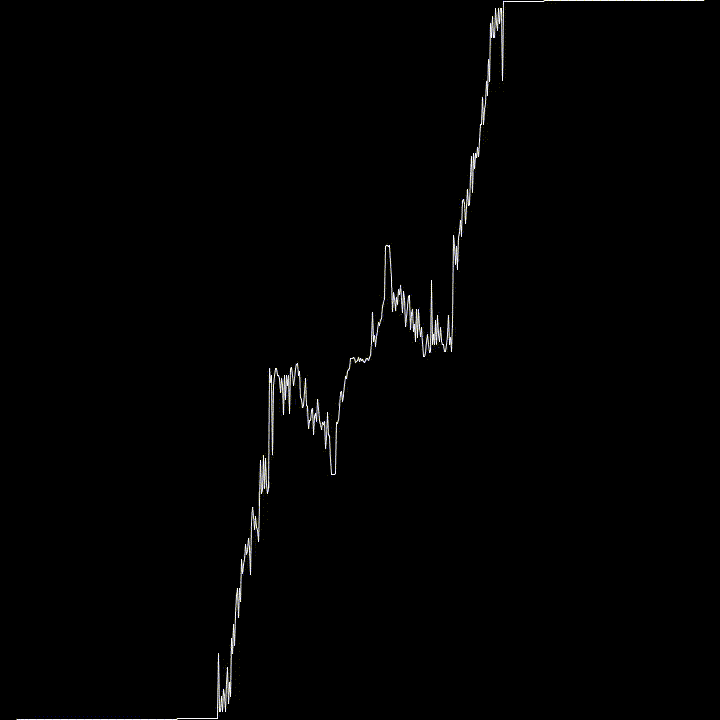
Today, just a quickie. The Devil’s Staircase (or Cantor Function) is a particular “pathological” function. It grows from 0 to 1 as $x$ goes from 0 to 1, but it’s derivative are 0 almost everywhere. Meaning, that everywhere you zoom, you’ll get a flat line. Yet it goes up. Yet it’s flat almost everywhere ! Code? Here!.

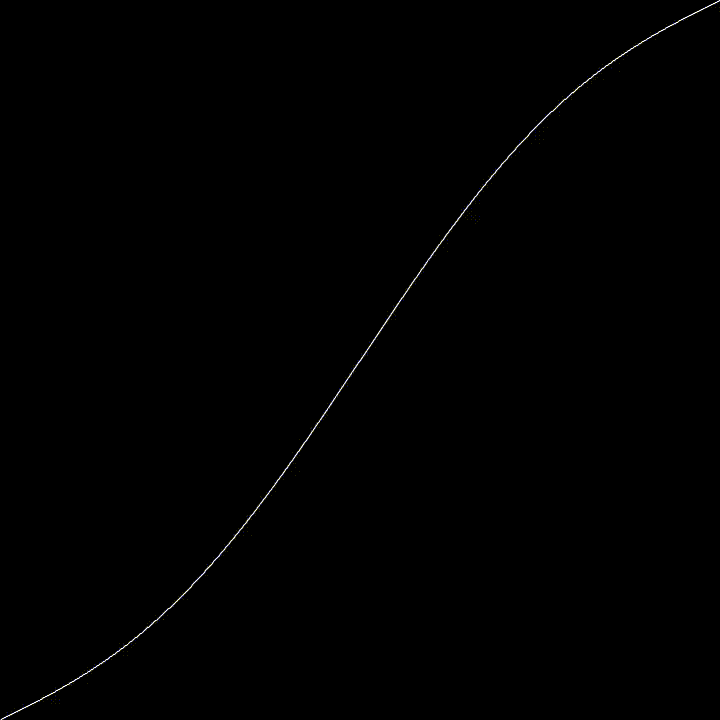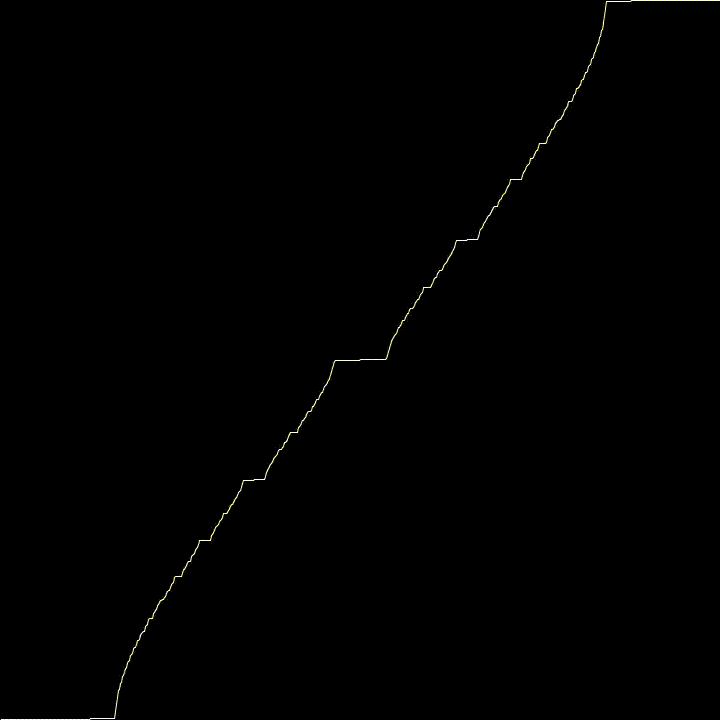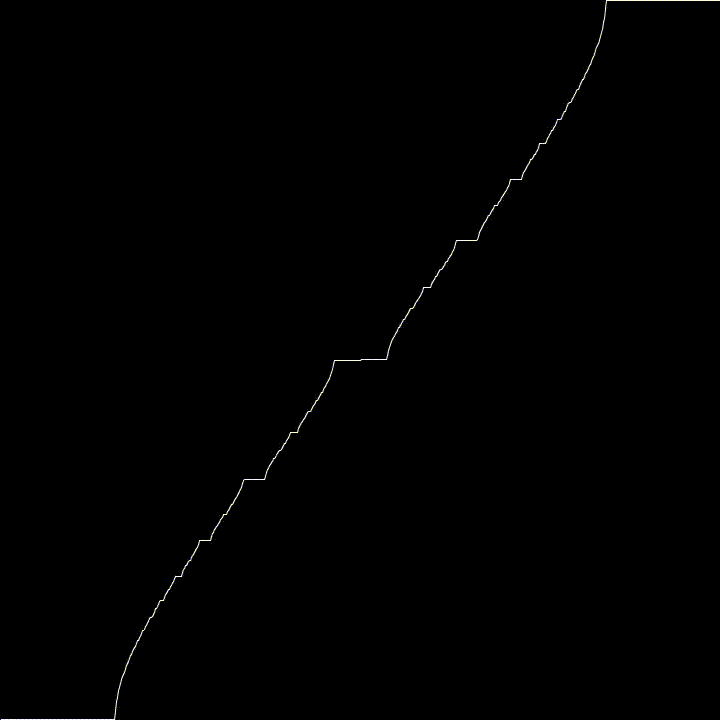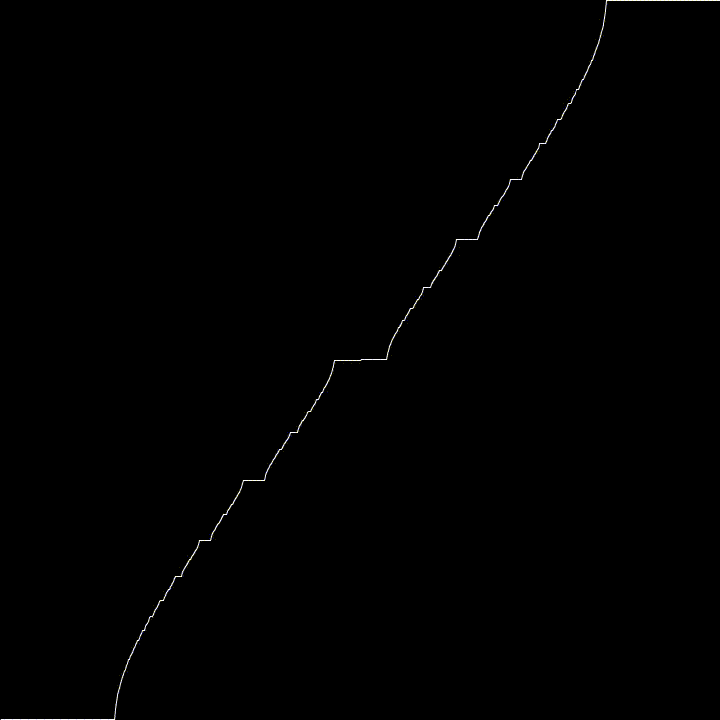
Here, we generate the Devil’s Staircase using a particular Circle Map

$$\phi_{n+1} = \phi_n - \frac{K * sin(2 * \pi * phi_n)}{2 * \pi} $$

Using $K = 1$ this map converge to the Cantor Function as $n \rightarrow \infty$. This is why it wiggles a bit.

For fun, I used varying values of K to see what kind of effects it would have. It tends towards the Cantor Function, then goes all weird.